Archive for septiembre 2014
ESTRUCTURAS DE CONTROL.
Por lo general, en un programa las
instrucciones se ejecutan una después de otra en el orden en que están
escritas. Este proceso se conoce como ejecución secuencial.
Las estructuras de control nos permiten
controlar el flujo del programa: tomar decisiones, realizar acciones
repetitivas etc. Dependiendo de unas condiciones que nosotros mismos
establezcamos.
ESTRUCTURA IF-ELSE.
Quizá la estructura de control más
básica y la más utilizada sea if-else, este seria un ejemplo de cómo se emplea
en la programación.
if (condición) {
//
instrucciones que hay que ejecutar si la condición es verdadera
} else
{
//
Instrucciones que hay que ejecutar si la condición es falsa
}
ESTRUCTURA
FOR.La estructura if-else no es muy
eficiente cuando se dedica a ejecutar de forma repetitiva una instrucción, la
estructura if-else solamente se muestra una vez el mensaje en pantalla, esta
estructura no se repite y la comprobación de la condición solo se realiza una
sola vez, por otra parte la estructura for permite realizar varias repeticiones
de forma sencilla, también llamadas bucles. No obstante, su definición formal
no es tan sencilla como la del if.For(iniciación; condición; actualización)La idea del funcionamiento de
un bucle for es la siguiente. “mientras la condición indicada se siga
cumpliendo, repite la ejecución de las instrucciones definidas dentro del for.
Además, después de cada repetición, actualiza el valor de las variables que se
utilizan en la condición”.La iniciación: es la zona en la
que se establece los valores iniciales de las variables que controlan la repetición.La condición: es el único
elemento que decide si continúa o se detiene la repetición.La actualización: es el nuevo
valor que se asigna después de cada repetición a las variables que controlan la
repetición.CONCLUSIÓN:Es importante conocer el
funcionamiento de cada instrucción para programar y darles el uso apropiado a
cada una de ellas para obtener un buen programa sin errores, cada estructura
tiene características similares pero en ocasiones nos es más conveniente el
usar una o la otra.
LÓGICA
BOOLEANA.
La lógica
booleana es un sistema basado en la lógica matemática, que se denomina álgebra
booleana. Esta designación hace referencia al matemático inglés George Boole.
Sirve para crear reglas o expresiones lógicas.
USOS DE LA LÓGICA BOOLEANA
La lógica booleana se utiliza en:
·
Selección
de ledgers
·
Report
Writer
·
Rollups
·
Validación
·
Sustitución
EXPRESIONES DE LÓGICA BOOLEANA
Una expresión de
lógica booleana es una sentencia lógica, que puede ser verdadera o falsa. A
continuación, unos ejemplos de expresiones verdaderas y falsas:
1.
2 + 2 = 4 (TRUE)
2.
10 < 6 (FALSE)
Las
expresiones lógicas se pueden enlazar mediante operadores.
Un operador enlaza expresiones lógicas y define el
modo en que éstas deben procesarse.
· A ND (Y)
(conjunción):
Con este operador, las dos expresiones que se
enlazan deben ser verdaderas para que la expresión combinada lo sea.
·
OR (O:
conjunción disyuntiva)
Con este operador, por lo menos una de las
expresiones debe ser verdadera para que la expresión combinada sea verdadera.
·
NOT (NO:
negación)
Con este operador, la expresión que sigue al
operador NOT debe ser falsa para que la expresión sea verdadera.
·
NAND (NOT
AND)
Con este operador, por lo menos una de las
expresiones debe ser falsa para que la expresión combinada sea verdadera.
·
NOR (NOT
OR)
Con este operador, las dos expresiones que se
enlazan deben ser falsas para que la expresión combinada sea verdadera.
CONCLUSIÓN:
La lógica booleana se refiere a un sistema lógico
matemático que nos sirve principalmente para definir formas de intersección
entre conjuntos, además una expresión lógica se define como una acción o hecho
que puede ser falso o verdadero.
Operadores lógicos.
|
SÍMBOLO
|
SIGNIFICADO
|
EJEMPLO
|
|
=
|
Igual que
|
A=B
|
|
>
|
Mayor que
|
A>B
|
|
<
|
Menor que
|
A<B
|
|
>=
|
Mayor o igual que
|
A>=B
|
|
<=
|
Menor o igual que
|
A<=B
|
|
<>
|
Distinto que
|
A<>B
|
|
NO (not)
|
No se cumple que
|
NO A=B
|
|
Y (and)
|
Y se cumple que
|
A = B y H > M
|
|
O (or)
|
O se cumple que
|
A = B ó H > M
|
Operadores aritméticos.
|
OPERADOR
|
NOMBRE
|
EJEMPLO
|
DESCRIPCIÓN
|
|
+
|
Suma
|
5 + 6
|
Suma dos números
|
|
-
|
Sustracción
|
7 - 9
|
Resta dos números
|
|
*
|
Multiplicación
|
6 * 3
|
Multiplica dos números
|
|
/
|
División
|
4 / 8
|
Divide dos números
|
|
%
|
Módulo: el resto después de la división
|
7 % 2
|
Devuelve el resto de dividir ambos números, en este
ejemplo el resultado es 1
|
|
++
|
Incremento.
|
a++
|
Suma 1 al contenido de una variable.
|
|
--
|
Decremento.
|
a--
|
Resta 1 al contenido de una variable.
|
|
-
|
Invierte el signo de un operando.
|
-a
|
Invierte el signo de un operando.
|
CONCLUSIÓN:
Los operadores lógicos y aritméticos nos son de gran
ayuda para poder realizar y comprender distintos programas, ya que en la
programación son necesarios y están estrechamente relacionados en la toma de
decisiones para realizar distintas acciones.
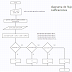
Estos tres diagramas de flujo fueron hechos
en un software simulador (DFD).
El primero consta de ingresar un número
cualquiera y el programa se encarga de descifrar si se trata de un número par o
un número impar.
El segundo diagrama de flujo es de un
cajero automático que permite consultar saldo y retirar un monto máximo de $5,000 pesos, despachando billetes con valores
de $500, $200, $100, $50 y $20.
Por último el tercer diagrama de flujo
consta de ingresar tres números distintos y el programa se encarga de imprimir
el número menor y el número mayor.
Como conclusión existen distintos
programas que facilitan el crear diagramas de flujo y son de mucha ayuda ya que
programas como estos (DFD), permiten la simulación del diagrama de flujo
creado.